JSP作为NP-难问题,基于数学模型的方法只能求解小规模问题,调度规则求解速度快但效果一般。因此现在的研究大多采用遗传算法等智能优化算法求解JSP问题以期望在合理时间内获得满意解。局部搜索是智能优化算法取得高质量解的关键,而邻域结构作为局部搜索的核心极大影响算法的性能。
「 1. 智能优化算法在作业车间调度中的应用 」
局部搜索算法能很好地克服了智能优化算法易陷入局部最优的缺点。因此,越来越多的研究人员将局部搜索算法引入其他算法框架求解JSP问题。Zhang等[1]将模拟退火算法和禁忌搜索算法相结合求解JSP问题。Peng等[2]将禁忌搜索算法引入路径重连算法框架求解JSP问题。路径重连算法增加了种群的多样性,将种群中的个体分散到解空间各处,更有利于个体执行禁忌搜索操作。Gonçalves和Resende[3]将禁忌搜索算法引入遗传算法框架求解JSP问题。遗传算法和禁忌搜索算法的结合很好地平衡了混合算法的全局搜索和局部搜索能力。将局部搜索算法与其他算法组合,能有效扩大算法的搜索空间,增强算法的全局搜索能力。因此,运用混合算法求解JSP问题逐渐成为了研究的热点。
「 2. 邻域结构在作业车间调度中的应用 」
邻域结构是否合理对局部搜索算法的效果有着直接的影响。在调度问题中,一般邻域结构的移动都是通过对关键路径上的工序产生小的扰动产生,只有如此才有可能缩短当前解的最大完工时间。
最著名的邻域结构是基于关键块的N5[4]、N6[5]和N7[6]邻域结构。N5邻域结构的设计如下:①若是第一个关键块,则交换块尾的两道工序;②若是最后一个关键块,则交换块首的两道工序;③若既不是第一个关键块,也不是最后一个关键块,则交换块首的两道工序和块尾的两道工序。图1是N5邻域结构的示意图。N6邻域结构是N5邻域结构扩展,进一步考虑了将关键块内部的工序移动到关键块的块首和块尾,但由于在作业车间调度问题中存在有不可行解的情况,因此需要在满足一定的约束条件的基础上,才能将内部工序移动到块首或块尾进行加工。图2是N6邻域结构的示意图。N7邻域结构在N6邻域结构的基础上,增加了将关键块块首和块尾的工序移动到关键块内部,同样,为了避免不可行解的出现,N7也需要满足与N6相同的约束条件。图3是N7邻域结构的示意图。
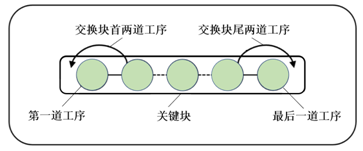
图1 N5邻域结构
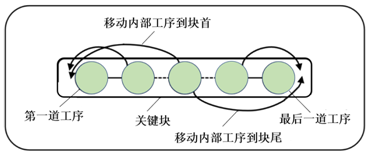
图2 N6邻域结构
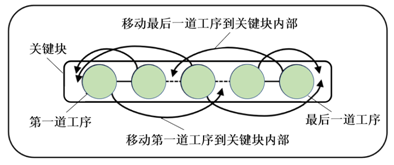
图3 N7邻域结构
N6和N7中的约束条件能够确保移动后产生的结果为可行解的充分条件,但仍然存在大量移动后的结果为可行解,但并不满足N6和N7中的约束条件,即这些约束条件为保证可行解的充分非必要条件。为了探究保证产生可行解的充分必要条件,首先要了解由可行解产生不可行解的充分必要条件,然后就可以反推出产生可行解的充分必要条件。
「 3. 基于遗传算法求解作业车间调度问题[8] 」
遗传算法基于自然界的进化规律而得到,由种群、选择、交叉和变异算子等部分组成,需要建立从染色体基因到个体外部特征的映射,即完成相应的编解码工作,编解码方式对算法性能有着重要影响。遗传算法的特性使其非常适合求解组合优化问题,在JSP的研究中应用广泛。
1)编码与解码
编码就是解的遗传基因表示,它是遗传算法实施优化过程中遇到的首要问题,是为了实现交叉、变异等类似于生物界的遗传操作,也是应用成功与否的关键之一。编码过程必须考虑染色体的合法性、可行性和有效性,以及对问题解空间表达的完全性,直接影响算法求解速度、计算精度等性能。良好的编码方式有利于在后续遗传操作中产生可行解,提高执行效率;否则,经过遗传操作会产生不可行解,需要一定的修补措施,这样就降低了执行效率。
本文采用Gen等[7]提出的基于工序的编码方式进行编码,染色体的长度等于所有工件的工序之和。每一个基因用工件号直接编码,工件号出现的顺序表示该工件工序间的先后加工顺序,即对染色体从左到右进行编译,对于第j次出现的工件号,表示该工件i的第j道工序,并且工件号的出现次数等于该工件的工序总数。如此编码柔性很高,可满足调度规模变化、工件工序数不定等各种复杂情况,而且任意置换染色体中的顺序后总能得到可行调度。假设染色体的编码是[2, 2, 1, 1, 2],则其中第一个2表示工序O21,第二个2表示工序O22,以此类推,转换成各工序的加工顺序为O21→O22→O11→O12→O23。
举例说明[8],表1为一个3×3的JSP问题,假设它的一个染色体为[2 1 1 3 1 2 3 3 2],其中1表示工件J1,2和3意义相同。染色体中的3个1依次表示工件J1的3道工序,分别为工序1、工序2和工序3;此染色体对应的机器分配为[3 1 2 2 3 1 3 1 2],对应的加工时间为[2 3 2 2 3 3 2 3 4]。图4表示该染色体解码成为对应机器和加工时间的方式[8]。按一般解码方式,依次从左到右将染色体上的工序都安排完为止,可生成的染色体对应的半活动调度方案,图5显示该染色体一般方式解码后所得半活动调度解[8],其中,机器1上的工件加工顺序为1-2-3,机器2上为1-3-2,机器3上为2-1-3,最大完工时间Makespan = 13。
表1 一个3×3的JSP问题
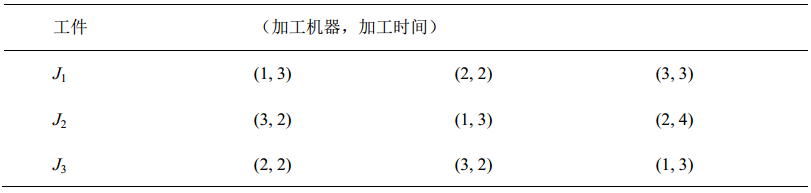
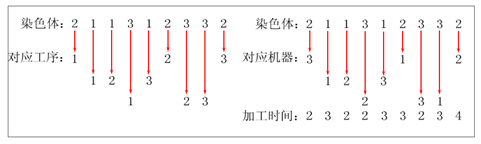
图4 解码方式
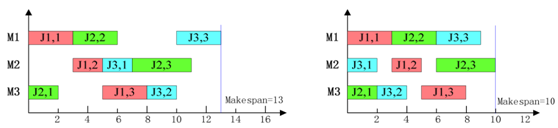
图5 半活动解码图6活动解码
按一般解码方式只能得到半活动调度,而不是活动调度。本文介绍一种插入式贪婪解码算法[8],能保证染色体经过解码后生成活动调度。插入式贪婪解码算法描述如下:首先将染色体看作工序的有序序列,根据工序在该序列上的顺序进行解码,序列上第1道工序首先安排加工,然后取序列上第2道工序,将其插入到对应机器上最佳可行的加工时刻安排加工,以此方式直到序列上所有工序都安排在其最佳可行的地方。按插入式贪婪解码算法,该染色体解码后可生成图6所示的活动调度解[8]。其中,机器1上的工件加工顺序为1-2-3,机器2为3-1-2,机器3为2-3-1,最大完工时间Makespan减少为10。然后,可以获得该活动调度对应的染色体[2 1 3 1 2 2 3 1 3]。
2)交叉算子
交叉的目的是利用父代个体经过一定操作组合后产生新个体,在尽量降低有效模式被破坏的概率基础上对解空间进行高效搜索。交叉操作是主要的遗传操作,遗传算法的性能在很大程度上依赖于所使用的交叉操作,它决定了算法的全局搜索能力。在设计交叉操作是必须满足可行性、特征的有效继承性、完全性和信息非冗余性等指标。特征的有效继承性保证父代中的优良信息能够保留到子代;信息非冗余性保证子代中不会产生过多无用信息,这两个特征在交叉操作设计中是两个重要指标。遗传算法中常用的交叉操作有单点交叉(SPX),多点交叉(MPX),均匀交叉(UX),基于工件顺序的交叉(JOX)和基于工件优先顺序的交叉(POX)等。本文采用的POX交叉操作,其具体的流程如下[8]:
步骤1 随机划分工件集{1, 2, 3, …, n}为两个非空的子集J1和J2。
步骤2 复制Parent1包含在J1的工件到Children1,Parent2包含在J1的工件到Children2,保留它们的位置。
步骤3 复制Parent2包含在J2的工件到Children1,Parent1包含在J2的工件到Children2,保留它们的顺序。
图7说明了两个4个工件和3台机器调度问题的染色体交叉过程。两父代Parent1、Parent2交叉生成Children1染色体基因为[3 2 2 1 2 3 1 4 4 1 4 3 ],Children2染色体基因为[4 1 3 4 2 2 1 1 2 4 3 3]。可以看出经过POX交叉,Children1染色体保留了Parent1中工件{2, 3}和Parent2中工件{1, 4}的次序,Children2染色体保留了Parent2中工件{2, 3}和Parent1中工件{1, 4}的次序,使子代可能继承父代优良特征。
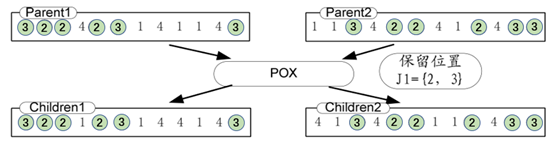
图7 POX交叉算子[8]
3)变异算子
在传统遗传算法中,变异是为了保持群体的多样性,它是由染色体较小的扰动产生。传统调度问题的遗传算法变异算子包括交换变异、插入变异和逆转变异。本文采用一种基于领域搜索的变异算子,如图8所示[8],它具有通过局部范围内搜索来改善子代的性能,具体步骤如下:
步骤1 设i= 0。
步骤2 判断i≤ popsize× pm是否成立(popsize是种群规模,pm是变异概率),是转到步骤3,否则转步骤6。
步骤3 取变异染色体上λ个不同的基因,生成其排序的所有领域。
步骤4 评价所有领域的调度适应值,取其中的最佳个体。
步骤5 i= i+ 1,转至步骤2。
步骤6 结束。
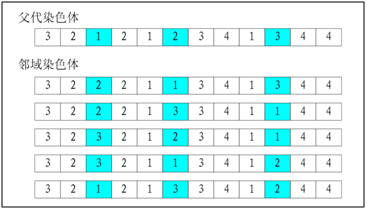
图8 变异算子[8]
4)遗传算法流程
在传统遗传算法中,交叉产生的子代总是被接受,即使它们适应度远低于父代的适应度,这可能造成优良解被丢失或破坏,而导致传统遗传算法易于早熟和收敛于较差解。本文设计一种改进子代产生模式的遗传算法,两父代交叉n次生成2n个后代,为了使子代更好地继承父代的优良特征,在从父代优的一个和所有2n个后代中选择最优一个的染色体作为下一代(两染色体适应度不同),这样既能将最优染色体保留到下一代,又能保证子代的多样性。这与人类繁殖类似,可使父代的优良特性更好地传递到下一代。求解JSP问题遗传算法的具体步骤如下:
步骤1 初始化随机产生P个染色体个体,P为种群规模。
步骤2 计算个体适应度,评价个体适应度值。
步骤3 判断是否达到终止条件,若满足则输出最优解,结束算法;否则转步骤4。
步骤4 按赌轮选择策略选取下一代种群。
步骤5a 按交叉概率Pc,对两父代个体交叉n次,从最优父代和所有后代中选择最优两染色体作为下一代。
步骤5b 按变异概率Pm选择个体,进行变异操作生成新个体。
步骤6 生成的新一代的种群,返回到步骤3。
5)实验结果与分析
本文用著名的Fisher和Thompson(FT)基准实例[9]对提出的改进遗传算法进行测试。具体遗传算法试验运行参数如下:种群规模P= 500,交叉概率Pc= 0.8,变异概率Pm= 0.01。实验结果见表7.5。
对于较简单FT6×6实例,遗传算法可以迅速收敛到下界,而对于难度较大的FT10×10也能在较短时间内收敛到下界。从表2可以看出对于FT基准实例[8],本文采用的遗传算法能取得较好的结果。
表2 FT基准实例测试结果[8]

遗传算法有着很强的并行性和全局寻优能力,但也有收敛速度慢、局部寻优能力较差等缺点,而禁忌搜索算法等一些启发式搜索算法则具有较强的局部搜索能力。结合不同算法的寻优思想对遗传算法进行改进,如在遗传框架内加入禁忌搜索操作可以提高算法的运行效率和求解质量。
「 4. 基于遗传与禁忌搜索混合算法求解作业车间调度问题[8] 」
1)交叉和变异操作
交叉和变异是遗传算法进化过程中的关键操作,它们决定着遗传算法全局搜索的能力。
2)禁忌搜索算法设计
禁忌搜索算法已经被有效地用于求解多种车间调度问题。该算法的特点是采用禁忌表来避免个体陷入局部最优。如果某一个体被禁忌表所禁止,那么它就不能被选为新解进入下一代。禁忌搜索算法包含以下几种元素:邻域结构、移动属性、禁忌表、特赦准则和终止条件。本文所采用的邻域结构是N7邻域结构。移动属性指工序间的移动操作。禁忌表用来禁止重复的移动操作。特赦准则是指当新解的Makespan比当前最优解更小时,即使新解的移动操作被禁止,仍然接受。终止条件是指当新解的Makespan达到了下界或算法到达了给定的迭代次数,则算法终止。禁忌搜索算法的流程如下:
步骤1 随机产生一个候选解x0,并设置当前最优解xb←x0。
步骤2 设置禁忌表T为Ø。
步骤3 基于N7邻域结构产生x0的多个邻域解,并选择Makespan最小且没有被禁忌,或满足特赦准则的解为x’。
步骤4 如果x’优于xb,设置xb← x’;同时设置x0← x’。
步骤5 更新禁忌表T。
步骤6 判断是否达到终止条件,若满足则输出最优解xb,结束算法;否则转步骤3。
3)混合算法的框架设计
遗传与禁忌搜索混合算法将“适者生存”的进化准则融入多起点禁忌搜索算法中,由遗传算法和对初始化及进化过程中产生的个体进行优化的强化禁忌搜索算法组成。从总体上分析,遗传算法用于执行全局探索,而强化禁忌搜索算法用于对有希望的区域进行集中搜索(局部探索)。由于遗传算法和禁忌搜索算法具有互补的特性,混合算法能够超越这两种算法单独使用。求解JSP问题的遗传与禁忌搜索混合算法流程如下:
步骤1 种群初始化并设代数i=1。
步骤2 对种群适应度值进行评估。
步骤3 判断是否满足终止条件?满足则跳转至步骤6;否则跳转至步骤4。
步骤4 更新种群:首先使用遗传算子(选择、交叉和变异)更新种群;然后对种群中每个个体使用禁忌搜索操作提高解的质量。
步骤5 设i=i+1,并返回步骤2。
步骤6 输出最优个体。
4)实验结果与分析
在混合算法中,遗传算法种群规模P、交叉概率Pc、变异概率Pm、进化代数和禁忌搜索算法参数等由大量试验测试确定,以保证算法在解的质量和计算速度之间平衡。
本文从经典的FT[9]、LA[10]和ABZ[11]基准集中选取15个困难案例对遗传与禁忌搜索混合算法进行测试。混合算法的运行参数设置如下:种群规模P= 10,交叉概率Pc= 0.8,变异概率Pm=0.1,禁忌列表长度L= 10,未改进迭代次数ImproveIter = 100 × n(n为工件数)。标准测试每个实例连续运行10次,以计算实例平均适应度和平均运行时间。实验结果见表3。
表3 FT、LA和ABZ基准实例测试结果[8]
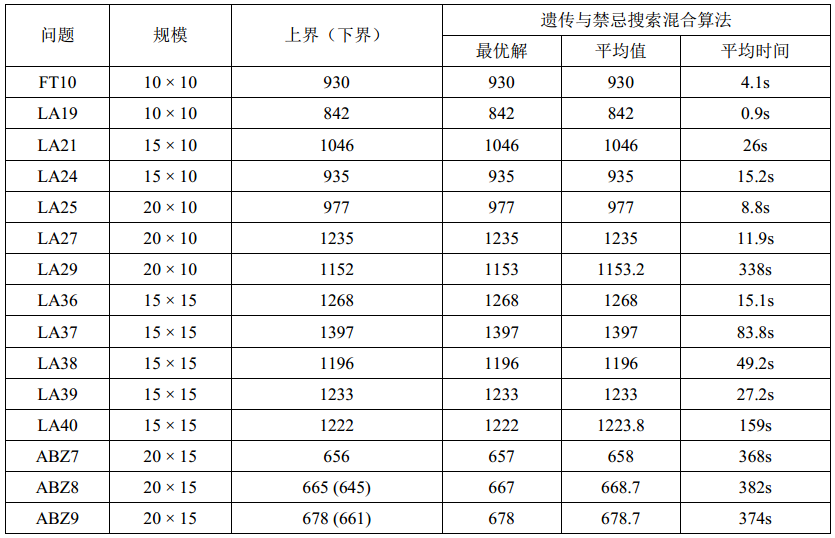
由表3可以看出,在最优解已知的13个实例中,混合算法获得了11个实例的最优解。实验结果验证了混合算法能有效地求解JSP问题。此外,10次运行获得的平均值与最优解的差距很小,反映了混合算法的鲁棒性极强。对于这15个困难的实例,混合算法都能在很短的时间内获得最优(或近似最优)解,显示了混合算法的高效性。
参考文献
[1]ZHANG C Y, LI P G, RAO Y Q, et al. A very fast TS/SA algorithm for the job shop scheduling problem. Computers & Operations Research, 2008, 35(1): 282-294.
[2]PENG B, LÜ Z, CHENG T C E. A tabu search/path relinking algorithm to solve the job shop scheduling problem. Computers & Operations Research, 2015, 53: 154-164.
[3]GONÇALVES J F, RESENDE M G C. An extended Akers graphical method with a biased random‐key genetic algorithm for job‐shop scheduling. International Transactions in Operational Research, 2014, 21(2): 215-246.
[4]NOWICKI E, SMUTNICKI C. A fast taboo search algorithm for the job shop problem. Management science, 1996, 42(6): 797-813.
[5]BALAS E, VAZACOPOULOS A. Guided local search with shifting bottleneck for job shop scheduling. Management science, 1998, 44(2): 262-275.
[6]ZHANG C Y, LI P G, GUAN Z L, et al. A tabu search algorithm with a new neighborhood structure for the job shop scheduling problem. Computers & Operations Research, 2007, 34(11): 3229-3242.
[7]GEN M, TSUJIMURA Y, KUBOTA E. Solving job-shop scheduling problems by genetic algorithm // Proceedings of IEEE International Conference on Systems, Man and Cybernetics. IEEE, 1994, 2: 1577-1582.
[8]张超勇.基于自然启发式算法的作业车间调度问题理论与应用研究[D].武汉:华中科技大学. 2006.
[9]FISHER H. Probabilistic learning combinations of local job-shop scheduling rules. Industrial scheduling, 1963: 225-251.
[10]LAWRENCE S. Resouce constrained project scheduling: An experimental investigation of heuristic scheduling techniques (Supplement). Graduate School of Industrial Administration, Carnegie-Mellon University, 1984.
[11]ADAMS J, BALAS E, ZAWACK D. The shifting bottleneck procedure for job shop scheduling. Management science, 1988, 34(3): 391-401.